February 8th, 2016
|
So far we’ve applied the Work-Energy Theorem to a flying object, namely, Santa’s sleigh, and a rolling object, namely, a car braking to avoid hitting a deer. Today we’ll apply the Theorem to a falling object, that coffee mug we’ve been following through this blog series. We’ll use the Theorem to find the force generated on the mug when it falls into a pan of kitty litter. This falling object scenario is one I frequently encounter as an engineering expert, and it’s something I’ve got to consider when designing objects that must withstand impact forces if they are dropped.

Applying the Work-Energy Theorem to Falling Objects
Here’s the Work-Energy Theorem formula again,
F × d = ½ × m × [v22 – v12]
where F is the force applied to a moving object of mass m to get it to change from a velocity of v1 to v2 over a distance, d.
As we follow our falling mug from its shelf, its mass, m, eventually comes into contact with an opposing force, F, which will alter its velocity when it hits the floor, or in this case a strategically placed pan of kitty litter. Upon hitting the litter, the force of the mug’s falling velocity, or speed, causes the mug to burrow into the litter to a depth of d. The mug’s speed the instant before it hits the ground is v1, and its final velocity when it comes to a full stop inside the litter is v2, or zero.
Inserting these values into the Theorem, we get,
F × d = ½ × m × [0 – v12]
F × d = – ½ × m × v12
The right side of the equation represents the kinetic energy that the mug acquired while in freefall. This energy will be transformed into Gaspard Gustave de Coriolis’ definition of work, which produces a depression in the litter due to the force of the plummeting mug. Work is represented on the left side of the equal sign.
Now a problem arises with using the equation if we’re unable to measure the mug’s initial velocity, v1. But there’s a way around that, which we’ll discover next time when we put the Law of Conservation of Energy to work for us to do just that.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: energy, engineering expert, falling objects, Gaspard-Gustave de Coriolis, impact forces, kinetic energy, law of conservation of energy, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury | Comments Off on Applying the Work-Energy Theorem to Falling Objects
January 29th, 2016
|
I’m sometimes called upon to render an engineering expert opinion on auto accidents, and in our last blog we stretched this application to a scenario in which Santa’s sleigh collided with the opposing force of a strong wind. At that time we used the Work-Energy Theorem to calculate the amount of food energy Rudolph and his team required to regain speed and get back on schedule. Today we’ll use the Theorem to analyze the forces at play in another deer scenario and calculate the braking distance a car needs to avoid hitting one on the highway.
The average sedan has a mass of about 1,500 pounds, or 680 kilograms. In our example it’s driving down the highway at a speed, or velocity, of 30 miles per hour, which equates to it covering a distance of 13.3 meters, or just under 44 feet, per second.
A deer jumps onto the highway, 60 meters in front of the car. The alert driver slams on the brakes, which exert 1200 Newtons of stopping force on the car. If you’ll recall from past blogs in this series, the Newton is the metric unit used to measure force.
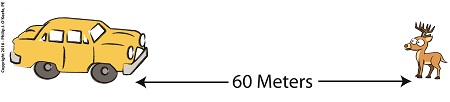 What is Safe Braking Distance? What is Safe Braking Distance?
Did Bambi survive? Let’s use the Work-Energy Theorem to find out. Here it is again,
F × d = ½ × m × [v22 – v12]
where, F is the braking force used to slow a car of mass m, from an initial velocity of v1 to a final velocity of v2 in a braking distance, d. The car will eventually come to a complete stop as the driver attempts to avoid hitting the deer, so its final velocity, v2, will be zero. The Work-Energy Theorem is most often stated in terms of metric units, the measuring unit of choice in the scientific community, and we’ll follow suit with our math.
Inserting these values into the equation, we get,
[1200 Newtons] × d
= ½ × [680 kilograms] × [(0)2 – (13.3 meters per second)2]
Using algebra to solve for d, the braking distance, we arrive at,
d = ½ × [680 kilograms] × [(0)2 – (13.3 meters per second)2] ÷ [1200 Newtons]
d = 50.11 meters
The car stopped 50.11 meters from the point when the driver slammed on his brakes, just about 10 meters short of hitting the deer. Bambi lives to leap another day!
Next time we’ll use the Work-Energy Theorem to assess the fate of the falling coffee mug we introduced in past blogs when we opened our discussion on the different forms of energy.
Copyright 2016 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: automobile, braking distance, braking force, engineering expert, mass, Newtons, velocity, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Personal Injury | Comments Off on Applying the Work-Energy Theorem to Braking Distance
January 20th, 2016
|
In my work as an engineering expert I’ve never had to convert Joules of work-energy into calories, but that’s exactly what we’ll be doing together today. Last time we applied the Work-Energy Theorem to the progress of Santa’s sleigh and found that an opposing wind force of 3848.7 Newtons –or 865.2 pounds for those of us who are American– slowed his team from an initial velocity of 90 meters per second to a final velocity of 40 meters per second and that it happened over a distance of 760 meters. Today we’ll see how many calories the reindeer need to expend to get them back up to full delivery speed.

Prancer Loves Oats
Now we know that Santa successfully made all his deliveries on time this past Christmas, so that means that at some point his reindeer team was able to get back up to full sleigh-flying speed. They did it by expending extra energy. We’ll use the Work-Energy Theorem to find out how much energy that equates to. Here’s the Theorem again,
W = ½ × m × [v22 – v12]
where W is the work/energy required to speed up the sleigh team’s mass, m, from an initial velocity v1 to a final velocity v2. For a refresher on the special relationship between work and energy, see our past blog on the subject.
If Santa’s sleigh has a mass of 900 kilograms and its speed must increase from 40 to 90 meters per second, then the work required to do so is calculated as,
W = ½ × (900 kilograms) × [(90 meters/second)2 – (40 meters/second)2]
W = ½ × (900 kilograms) × (6,500 meters2/second2)
W = 2,925,000 kilogram2 · meters2 per second2 = 2,925,000 Joules
So Rudolph and his buddies had to expend 2,925,000 Joules of energy to perform 2,925,000 Joules of work. To understand where Rudolph and his team got that energy, we must state things in terms of nutritional value, that is, units of calories.
Did you know that 1 calorie is equal to 4,184.43 Joules? Applying that equivalency to our situation we get,
Nutritional Energy Required = (2,925,000 Joules) × (4,184.43 Joules/calorie)
= 699.02 calories
The net result is Santa’s team expended a total of 699.02 calories for all the reindeer to regain their full speed of 90 meters per second. That’s the nutritional energy found in slightly more than one cup of oats. Now everybody knows that Santa takes good care of his reindeer, so undoubtedly they were fed plenty of oats and hay before takeoff. This was stored in their body fat for future, on-demand use.
Sadly, Christmas is over, and it’s time to get back to the more mundane aspects of life. Next time we’ll apply the principles behind the Work-Energy Theorem to calculate the braking force required to stop a car in motion.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: calories, energy, engineering expert, Joules, mass, speed, velocity, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Work and Energy, Speed, and Calories
January 11th, 2016
|
Last time my engineering expertise was put to the test when it was discovered that Santa’s sleigh was being hampered by a strong gust of wind. At that time we introduced the Work-Energy Theorem to determine how strong the wind’s opposing force was, and today we’ll work with the Theorem to compute just what Rudolph was up against. Here again is the expanded, workable version of the Work-Energy Theorem as introduced last time,
F × d = ½ × m × [v22 – v12]
where F is a force acting upon a moving object of mass m over a distance d to slow it from an initial velocity of v1 to a final velocity of v2.
Applying the Theorem to the dynamics at play in Santa’s situation, F is the opposing wind force, which acts over a distance, d, to slow his sleigh from an initial velocity of v1 to a final velocity, v2, thus presenting Rudolph and his buddies with a real delivery challenge.
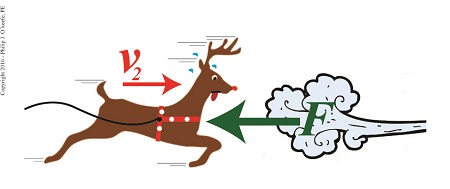 Rudolph Struggles Against a Fierce Wind Rudolph Struggles Against a Fierce Wind
If we know that Santa, his sleigh and reindeer have a combined mass of 900 kilograms — which is pretty standard for a fully loaded sleigh and reindeer team — and their initial velocity was 90 meters per second, final velocity 40 meters per second, and the distance over which the slowing took place was 760 meters, then the formula to calculate the opposing wind force becomes,
F × d = ½ × m × [v22 – v12]
F = ½ × m × [v22 – v12] ÷ d
F = ½ × (900kg) × [(40 meters/sec)2 – (90 meters/sec)2] ÷ 760 meters
F = -3848.7 Newtons = -865.2 Pounds
The minus sign signifies that the wind must exert an opposing force of 865.2 pounds in order to slow Santa’s sleigh down.
In order for Santa to get back on his delivery schedule, Rudolph is going to have to make up for lost time by expending extra energy. We’ll see how he does that next time.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, engineering expert, force, mass, Newtons, pounds, velocity, Work-EnergyTheorem
Posted in Engineering and Science, Expert Witness, Innovation and Intellectual Property, Personal Injury | Comments Off on The Work-Energy Theorem Applied to Santa’s Sleigh
January 1st, 2016
|
As an engineering expert I’ve applied the Work-Energy Theorem to diverse situations, but none as unique as its most recent application, the progress of Santa’s sleigh. Last week we saw how Santa and his reindeer team encountered a wind gust which generated enough force to slow them from an initial velocity of v1 to a final velocity, v2, over a distance, d. Today we’ll begin using the Work-Energy Theorem to see if Santa was able to keep to his Christmas delivery schedule and get all the good boys and girls their gifts in time.

Before we can work with the Work-Energy Theorem, we must first revisit the formula it’s predicated upon, de Coriolis’ formula for kinetic energy,
KE = ½ × m × v2 (1)
where, KE is kinetic energy, m is the moving object’s mass, and v its velocity.
The equation behind the Work-Energy Theorem is,
W = KE2 – KE1 (2)
where W is the work performed, KE1 is the moving object’s initial kinetic energy and KE2 its final kinetic energy after it has slowed or stopped. In cases where the object has come to a complete stop KE2 is equal to zero, since the velocity of a stationary object is zero.
In order to work with equation (2) we must first expand it into a more useful format that quantifies an object’s mass and initial and final velocities. We’ll do that by substituting equation (1) into equation (2). The result of that term substitution is,
W = [½ × m × v22 ] – [½ × m × v12] (3)
Factoring out like terms, equation (3) is simplified to,
W = ½ × m × [v22 – v12] (4)
Now according to de Coriolis, work is equal to force, F, times distance, d. So substituting these terms for W in equation (4), the expanded version of the Work-Energy Theorem becomes,
F × d = ½ × m × [v22 – v12] (5)
Next time we’ll apply equation (5) to Santa’s delivery flight to calculate the strength of that gust of wind slowing him down.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: de Coriolis, distance, energy, engineering expert, force, kinetic energy, mass, velocity, wind force, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury | Comments Off on The Math Behind the Work-Energy Theorem
December 25th, 2015
|
I hope all the good little boys and girls got Santa’s presents, because his sleigh was spotted yesterday on radar moving at an alarmingly slow pace.
As the radar screen here shows, the progress of Santa and his reindeer had slowed from an initial velocity of v1 to a much slower velocity of v2 over the distance, d, he traveled from his workshop.
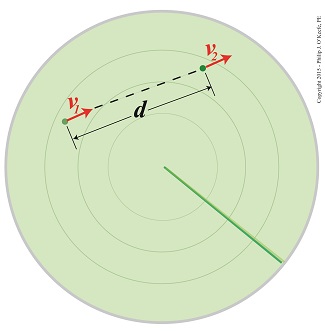
Santa’s Sleigh Tracked On Radar
Upon closer examination, the radar operator noted that the North Wind was especially powerful this year, which caused Rudolph and the gang to double their efforts to overcome its negative force.

Santa and His Reindeer Fighting The Wind
Did Santa make it in time to deliver Christmas presents? Find out next time, when we put the developing drama into the form of mathematical equations.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distance, force, velocity, work-energy theorem
Posted in Engineering and Science | Comments Off on The Work-Energy Theorem Affects Santa’s Sleigh!
December 18th, 2015
|
My work as an engineering expert sometimes involves computations of energy expended, as when I must determine how much energy is required to move something. But sometimes the opposite needs to be calculated, that is, how much energy is required to stop something already in motion. That’s the subject of today’s discussion, which we’ll approach by way of the Work-Energy Theorem.
The Work-Energy Theorem states that the work required to slow or stop a moving object is equal to the change in energy the object experiences while in motion, that is, how its kinetic energy is reduced or completely exhausted. Although we don’t know who to attribute the Theorem to specifically, we do know it’s based on the previous work of Gaspard Gustave de Coriolis and James Prescott Joule, whose work in turn built upon that of Isaac Newton’s Second Law of Motion.
Consider the example shown here. A ball of mass m moves unimpeded through space at a velocity of v1 until it is met by an opposing force, F. This force acts upon the ball over a travel distance d, resulting in the ball’s slowing to a velocity of v2.
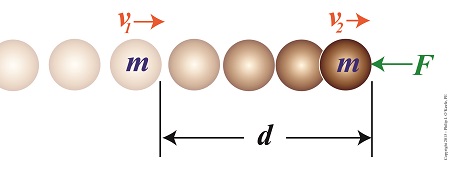
The Work – Energy Theorem Illustrated
Does the illustration make clear the Work-Energy Theorem dynamics at play? If not, return for the second part of this blog, where we’ll clarify things by getting into the math behind the action.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: energy, engineering expert witness, Gaspard-Gustave de Coriolis, Isaac Newton's Second Law of Motion, James Prescott Joule, kinetic energy, moving object, work, work-energy theorem
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Work-Energy Theorem — Background
December 10th, 2015
|
My work as an engineering expert has often required that I perform calculations to quantify the energy consumed by electric motors and steam turbines, such as when they work together at power plants to generate electricity. Today we’ll see how work and energy share an interesting relationship that is brought out by examining the units by which they are measured.
Last time we used de Coriolis’ formula to compute work to calculate the amount of work performed while pushing a loaded wheelbarrow a distance of 3 meters. We found that in order to move the wheelbarrow that distance, a gardener must exert a force equal to 534 Newton • meters of work. That relationship is shown here,
Work = 178 Newtons × 3 meters = 534 Newton • meters (1)

de Coriolis’ Formula to Compute Work
The Newton, as discussed previously in this blog series, is shorthand notation for metric units of force, and we’ll use those units today to demonstrate the special relationship between work and energy.
We’ll start by supposing that you’re unfamiliar with the Newton as a unit of measurement. In that case you’d have to employ longhand notation to quantify things, which means you’d be measuring units of force in terms of kilogram • meters per second2.
Putting equation (1) in longhand notation terms, we arrive at,
Work = 178 kilogram • meters per second2 × 3 meters (2)
Work = 534 kilogram • meters2 per second2 (3)
If you’ve been following along in this blog series, you’ll recognize that the unit of measurement used to compute work, namely, kilogram • meters2 per second2, is the same as was used previously to measure energy. That unit is the Joule, which is considerably less wordy.
Equations (2) and (3) bear out the interesting relationship between work and energy — they share the same unit of measure. This relationship would not be apparent if we only considered the units for work presented in equation (1).
So following standard engineering convention where work and energy are expressed in the same units, the work required to push the wheelbarrow is expressed as,
Work = 534 Joules
Yes, work and energy are measured by the same unit, the Joule. But, energy isn’t the same as work. Energy is distinguished from work in that it’s the measure of the ability to perform work. Stated another way, work cannot be performed unless there is energy available to do it, just as when you eat it provides more than mere pleasure, it provides your body with the energy required to perform the work of pushing a wheelbarrow through the garden.
Next time we’ll see how work factors into the Work Energy Theorem, which mathematically relates work to energy.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: de Coriolis' formula to compute work, electric motors, energy, engineering expert, generate electricity, joule, Newton meters, Newtons, power plants, steam turbines, unit of energy, units of force, work, work energy relationship, work required
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Work and Energy Share an Interesting Relationship
November 29th, 2015
|
Although I’m an engineering expert in the 21st Century, I often have to employ engineering principles that are centuries old. A case in point is Gaspard Gustave de Coriolis‘ formula to compute work, as set out in his Principle of Work. We’ll work with his formula today, and we’ll introduce a unit of measurement used to quantify work known as the Newton.
de Coriolis’ formula to compute work is used to determine the amount of work, that is, the amount of dynamic energy available to influence the movement of an object, and is calculated by the formula,
Work = Force × Distance
where F represents the force acting upon an object that travels a distance of D. Force is most often expressed in metric units as kilogram • meter per second2, a wordy expression which is more conveniently referred to as the Newton.
In the image below, F is the force of 178 Newtons exerted by the gardener to push his filled wheelbarrow a distance of 3 meters. The quantity 178 Newtons was obtained by way of direct personal experience working in my own garden. I’ve found that it takes approximately 40 pounds of force to push a wheelbarrow loaded with dirt across level ground. Because one pound of force is equal to 4.45 Newtons, the amount of force I exerted is expressed as,
[40 pounds of force] × [4.45 Newtons per pound force] = 178 Newtons

Work = Force × Distance
If 178 Newtons of force is required to push the wheelbarrow a distance of 3 meters, then the work performed is expressed as,
Work = 178 Newtons × 3 meters
= 534 Newton • meters
Next time we’ll explore the special relationship between work and energy and introduce another unit used to quantify work.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: de Coriolis' formula to compute work, distance, energy, engineering expert, force, Gaspard Gustave de Coriolis' principle of work, Newton, work formula
Posted in Engineering and Science, Expert Witness, Innovation and Intellectual Property, Personal Injury | Comments Off on de Coriolis’ Formula to Compute Work and the Newton
November 15th, 2015
|
I was recently retained as an engineering expert in a lawsuit in which I had to determine the force acting upon an object. In order to quantify that force, I employed Gaspard Gustave de Coriolis‘ Principle of Work, an engineering concept he introduced in his 1829 textbook, Calculation of the Effects of Machines. We’ll take our first look at de Coriolis’ Principle of Work today, along with the term he used to quantify work, the dynamode.
As a scientist living during the time of the great Industrial Revolution, de Coriolis was interested in lots of things, and he was particularly interested in quantifying the effort involved to accomplish tasks, like how many men, horses, or steam engines were required to move a stationary object. He defined this activity as work, and he hoped its study would lead to a broadly accepted engineering principle which could be applied across industrial functions.
According to de Coriolis, work is the force acting upon a stationary object which causes it to move, multiplied by the distance moved. Work could also be defined as the force acting upon an object already in motion, multiplied by the distance traveled before it comes to a stop.
To quantify work, de Coriolis proposed the dynamode as its unit of measure, a term which derives from the Greek words dynamis, meaning power, and odos, meaning path. He went on to define one dynamode as the amount of work required to lift an object with a mass of 1,000 Kg, or kilograms, one meter above the ground.
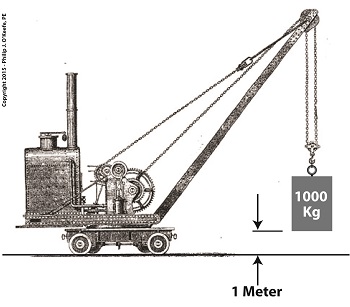
de Coriolis’ Dynamode Quantity
Catchy as it may sound, the word dynamode is all but forgotten today. But de Coriolis’ Principle of Work and his formula to calculate work remain to the present day as fundamental concept in engineering. We’ll present that formula next time.
Copyright 2015 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: de Coriolis’ Principle of Work, dynamode, engineering expert, joule, lawsuit, work
Posted in Engineering and Science, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on de Coriolis’ Principle of Work and Dynamode














